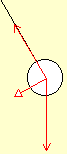
 Let's start with the pendulum stationary
at the top of its swing.
Let's start with the pendulum stationary
at the top of its swing.Gravity pulls down on the pendulum bob, and the cord pulls in - preventing itself being further stretched by the component of gravity acting along its length.
The resultant force (the "result" of adding these two) is at right angles to the cord, and the pendulum accelerates in this direction.
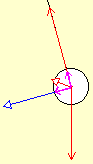 Once the
pendulum is moving the cord does more than oppose the component of gravity
along it; it also pulls the pendulum bob in to keep it on a circular path.
Once the
pendulum is moving the cord does more than oppose the component of gravity
along it; it also pulls the pendulum bob in to keep it on a circular path.
Splitting up the resultant force on the pendulum bob (into two magenta arrows) we can see it as a combination of one force pulling the pendulum in, and another accelerating it along its circular path.
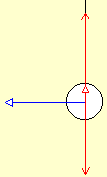 When the
pendulum reaches the bottom of its swing all forces are vertical (if friction
is zero); gravity pulling down, and the greater cord tension pulling up.
The resultant force is entirely the
centripetal force needed
to keep the pendulum on its circular path.
When the
pendulum reaches the bottom of its swing all forces are vertical (if friction
is zero); gravity pulling down, and the greater cord tension pulling up.
The resultant force is entirely the
centripetal force needed
to keep the pendulum on its circular path.As the pendulum climbs the other side there is again a growing component of the resultant force along the pendulum's path. But now it acts to slow the pendulum down - until it hangs stationary for a moment at the top of its swing the other side.
Changes in tension
On a swing
Laws of Motion